Apple serait donc actuellement en négociation avec les éditeurs de musique pour proposer un encodage sur 24 bits des titres vendus sur l'iTunes Store (lire iTunes Music Store : Apple veut passer en 24 bits). L'occasion pour nous de vous expliquer par le menu ce qu'est un son numérique, et en quoi cela change les choses.
Commençons par définir l'objet du délit : un son est une vibration de l'air. On peut en faire une représentation graphique avec en abscisse le temps et en ordonnée l'amplitude de la vibration : une onde plus grande aura un volume plus élevé, une courbe "tassée" en largeur représente un son aigu. Car c'est la fréquence de la vibration qui déterminera la hauteur de la tonalité. L'unité de mesure des fréquences est le hertz : 1 hertz correspond à une oscillation par seconde. Comme on le verra, nombre de paramètres concernant le son se mesurent en hertz, mais ne s'appliquent pas aux mêmes choses. Le la du diapason (ou de la tonalité du téléphone) a une fréquence de 440 Hz (la fréquence des notes de musique suit une augmentation logarithmique, le doublement d'une fréquence passe la note à l'octave supérieure). Bien que l'acuité auditive varie d'une personne à l'autre, il est généralement admis que l'oreille humaine est capable de percevoir des fréquences comprises entre 20 Hz et 20.000 Hz, avec une perte dans les aigus à mesure que l'on vieillit.
Physique amusante : un haut parleur diffuse une fréquence de 120 Hz dont les vibrations font danser ce liquide non-newtonien
L'enregistrement analogique d'un son est susceptible de stocker tout son spectre dans ses plus infimes détails, mais finit par s'altérer avec le temps et le nombre de copies successives. A l'inverse, un enregistrement numérique se limite à une résolution donnée qui perd par essence des subtilités, mais conservera son intégrité d'une copie à l'autre. Pour numériser un son, on applique une "grille" qui permet de stocker une valeur numérique : à un instant T correspond une amplitude sonore que l'on peut stocker sous forme de nombre.
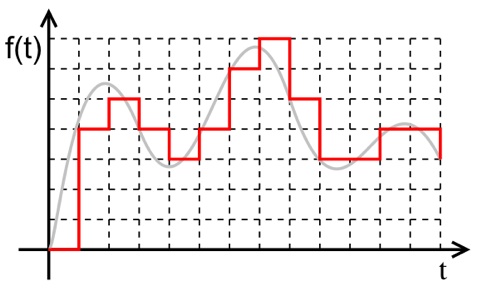
On procède de la sorte plusieurs fois par seconde, cela s'appelle l'échantillonnage. Mais puisqu'il est également ici question de fréquence d'échantillonnage, c'est à dire du nombre d'échantillons que l'on prélève par seconde, là aussi la mesure se donne en hertz, bien qu'elle n'ai pas de rapport direct avec la fréquence du son (c'est à dire la hauteur de la note). Ainsi, un la (440 Hz) pourra par exemple être échantillonné 1000 fois par secondes (et donc à 1 KiloHertz).
Toutefois, il existe bien une relation entre la fréquence sonore et la fréquence d'échantillonnage : le théorème de Nyquist-Shannon stipule que la fréquence d'échantillonnage doit être égale à au moins deux fois la fréquence maximale du signal. La raison en est simple : la période d'une onde passe par un point haut et un point bas, et il faut donc pouvoir capter ces deux extrêmes, soit prendre deux mesures par oscillation. Comme il est établi que l'oreille humaine peut percevoir des fréquences s'élevant jusqu'à 20.000 Hz, pour enregistrer la fréquence la plus haute il faudra donc l'échantillonner au moins 40.000 fois par seconde (et donc à 40 KHz). De fait, la fréquence d'échantillonnage sur CD audio est légèrement supérieure (44.100 Hz), afin de conserver correctement les fréquences non-harmoniques, sachant d'autre part que cette fréquence a été choisie pour sa compatibilité avec les systèmes vidéo (dans les premiers temps le signal était converti en signal vidéo pour être stocké sur cassettes u-matic pour l'envoi du master). Le son sur DVD est échantillonné à 48 KHz.
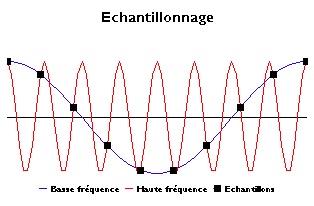
A noter toutefois qu'en environnement professionnel, on monte la fréquence d'échantillonnage à 96 KHz : cette meilleure définition offre une plus grande souplesse pour la manipulation du son avant le mixage définitif. C'est également la fréquence d'échantillonnage du son sur Blu-ray. On pourrait donc y enregistrer un ultrason d'une fréquence d'oscillation de 48 KHz, qui sera entendu par votre chien, mais pas par vous.
Voilà pour l'échelle temporelle, reste la mesure de l'amplitude en elle-même. Le nombre auquel correspond l'amplitude sonore à un instant T est encodé sur un nombre de bits donné. Il s'agit là d'une notion purement informatique : en fonction de cet encodage, l'amplitude sera numérisée plus ou moins finement. Ainsi, un encodage sur 8 bits permettra d'utiliser 256 valeurs différentes (soit 28, un bit ayant une valeur de 1 ou 0). Le standard pour le CD Audio est de 16 bits, soit 65.536 valeurs différentes possibles pour l'amplitude sonore. Sur un CD, chaque valeur de l'amplitude sera donc stockée sur 16 bits, soit deux octets, multipliés par 44.100 échantillons par seconde : une seconde de son stéréo sur CD occupe donc un peu plus de 172 Ko (rappelons que le son sur CD audio n'est pas compressé).
On affine donc la définition du son numérique en augmentant la valeur d'encodage (bitrate) et la fréquence d'échantillonnage. Une plus grande valeur d'encodage donnera une meilleure réponse dynamique du son, et une plus grande finesse dans les sons de faible amplitude. Une plus grande fréquence d'échantillonnage captera plus finement les variations de tonalité et d'harmoniques du son.
En passant le bitrate à 24 bits, l'amplitude du son serait ainsi plus fidèlement reproduite, sachant que les valeurs sont arrondies à l'unité la plus proche comme illustré plus haut : on passerait ainsi de 65.536 à 16.777.216 valeurs différentes possibles pour l'amplitude du son. Un grain 256 fois plus fin, permettant un écart plus grand entre l'onde la plus forte et la plus douce.

Mais la numérisation du son présente bien d'autres avantages que la seule fidélité de sa reproduction. Le traitement du signal numérique offre évidemment bien plus de liberté que sa contrepartie analogique, puisque l'avantage des nombres, c'est qu'ils se soumettent facilement aux mathématiques. Et c'est heureux, puisqu'un son en qualité CD prend une quantité de stockage dispendieuse (il faudrait une connexion internet d'au moins 1400 Kbps pour diffuser du son de cette qualité), un inconvénient facilement compensé par la compression de données. En supprimant les données redondantes ou superflues, en adaptant l'encodage en fonction du signal, ou encore en faisant appel à la psychoacoustique (l'étude scientifique de la perception sonore chez l'être humain), on peut ainsi conserver une qualité sonore apparemment similaire tout en utilisant un espace de stockage bien moindre.
Il existe différents systèmes de compression : certains sont non-destructifs, c'est à dire qu'ils restituent l'intégralité du signal après décompression, sans perte de données, mais au prix d'une moindre compression. Le célèbre MP3 (en réalité MPEG-1 Audio Layer 3), mis au point par l'institut allemand Fronhofer en 1993, est sans doute le codec destructif le plus connu. Il permet de diviser par 11 le volume de données sans que la perte de qualité induite ne soit trop gênante à l'écoute : ainsi, au lieu de 1400 Kilo-bits par seconde comme sur CD, le même son en MP3 n'utilisera plus que 128 Kilo-bits par seconde. Pour une musique donnée, c'est donc onze fois moins de stockage utilisé, ou encore onze fois moins de temps pour la télécharger, et à l'inverse, onze fois plus de musique à volume égal. A l'époque où le haut débit n'était encore qu'un rêve lointain et que les disques durs moyens n'alignaient encore péniblement que quelques centaines de méga-octets, l'économie s'avéra hautement appréciable.
En réalité ce taux de 128 Kbps est arbitraire et on peut choisir un taux de compression moindre au moment de la création du fichier MP3. D'autre part, la qualité sonore qui en résultera dépendra beaucoup du logiciel d'encodage, tous n'étant pas égaux sur les résultats obtenus. De fait, au fil des ans la musique a été encodée avec un taux de compression moindre (256 kbps), et iTunes ne propose sa musique qu'au format AAC, qui à taille égale avec le MP3 offre une meilleure qualité sonore, quoi que toujours dégradée par rapport à un signal non compressé.
Image Une